Die Produktionsfunktion beschreibt in der VWL die Menge des Outputs im direkten Verhältnis zur Menge des Inputs im Rahmen eines Produktionsverfahrens. Vereinfacht dient sie dem Zweck das optimale Verhältnis zwischen Input und Output zu bestimmen und so die Produktion zu optimieren.
Die Produktionsfunktion wird immer über die Art der Produktion bestimmt. Dafür gibt es zwei bekannte Arten – die substitutionelle und die limitationale Produktionsfunktion.
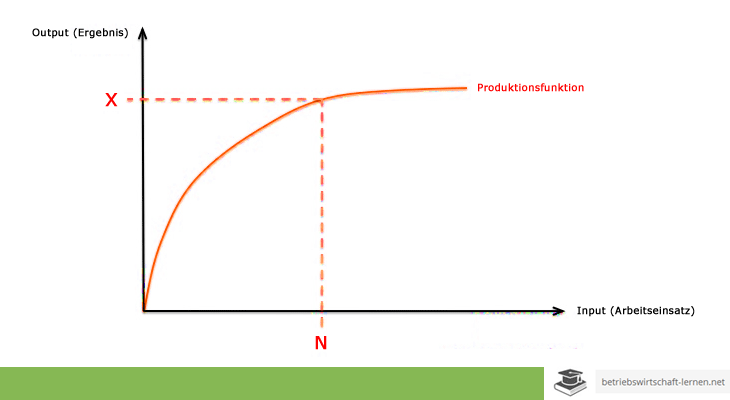
Substitutionale Produktionsfunktion
Die substitutionale Produktionsfunktion kommt immer dann zum Einsatz, wenn eines der Produktionsgüter ersetzt (substituiert) werden kann. Im Rahmen der Berechnung kann auch die jeweilige Substitutionalität berücksichtigt werden. Hier unterscheidet man dann zwischen der totalen und der periphären Substitutionalität.
Als dritte Variation kommt die konstante Substitutionalität im Rahmen von CES-Funktionen in Betracht.
Die substituionale Produktionsfunktion beruht im wesentlichen auf zwei Verfahren zur Berechnung:
Ertragsgesetzlich – Dies ist die älteste Produktionsfunktion, denn sie beruht auf den Erkenntnissen und Beobachtungen von Turgot und wurde ursprünglich von ihm als „Gesetz vom abnehmenden Bodenertrag“ bezeichnet. Sie zeigt auf, dass bei einem steigenden Einsatz von Input der Output zunächst steigt, später und ab einer bestimmten Menge an Input aber stetig abfällt.
Cobb-Douglas – Die Cobb-Douglas Funktion geht auf ihre Namensgeber Charles Wiggins Cobb und Paul Howard Douglas zurück. Bei ihr gibt es kein definiertes Produktionsmaximum und wird davon ausgegangen, dass ein steigender Input immer einen steigenden Output zur Folge hat.
Sie berücksichtigt aber den Tatbestand, dass ein gestiegener Input nicht unbedingt einen Output im selben Verhältnis zur Folge haben muss, sondern der Output im direkten Vergleich tendenziell eher sinkt.
Limitationale Produktionsfunktion
Bei der limitationalen Produktionsfunktion wird davon ausgegangen, dass für eine Steigerung des Ertrags eine Steigerung aller Produktionsfaktoren nötig ist. Dies gilt nicht wenn nur einer der Produktionsfaktoren im Überschuss vorhanden ist. Solange der Überschussfaktor vorhanden ist, ist zwar eine Steigerung der Produktion möglich aber keine Steigerung des Ertrags.
Um den Ertrag zu optimieren muss folglich das richtige Einsatzverhältnis eingehalten werden. Auch bei dieser Produktionsfunktion gibt es wieder zwei bekannte Schemata:
Linear-limitational – Hier stehen alle Produktionsfaktoren (Input und Output) zu einem festen Verhältnis zueinander.
Nichtlinear-limitational – Dieses Schema hat keine feste Definition und wird innerhalb der VWL noch recht kritisch, aber auch vielseitig bewertet und erforscht.
Bekannte Funktionen die als nichtlinear-limitational bezeichnet werden sind die „Gutenberg-Funktion„, oder die auf ihr aufbauende „Heinen-Produktionsfunktion“.
Allgemeines zu Produktionsfunktionen
Alle Arten der Produktionsfunktionen unterliegen einem steten Wandel. Aktuelle Themen sind vor allem die Umwelt als Produktionsfaktor oder die zunehmende Globalisierung und steigende Komplexität der Finanzwirtschaft, welche die Entwicklungen von Produktionsfunktionen zunehmend anspruchsvoller machen.
Produktionsfunktionen erfüllen aber ausnahmslos das mathematische Kriterium der additiven Separabilität und bestehen somit nur aus einfachen Summanden (= Funktion kann leichter zerlegt werden und die Ableitung ist unabhängig von anderen Variablen).
